Wer sich mit den verschiedenen Angeboten für Teslekope und das entprechende Zubehör beschäftigt wird immer wieder mit verchiedenen Kennzahlen konfrontiert. Was sich hinter diesen Kennzahlen verbirgt wird auf dieser Seite erläutert.
Zu folgenden Kennzahlen sind Informationen verfügbar:

|
|
|
Objektivöffnung
|
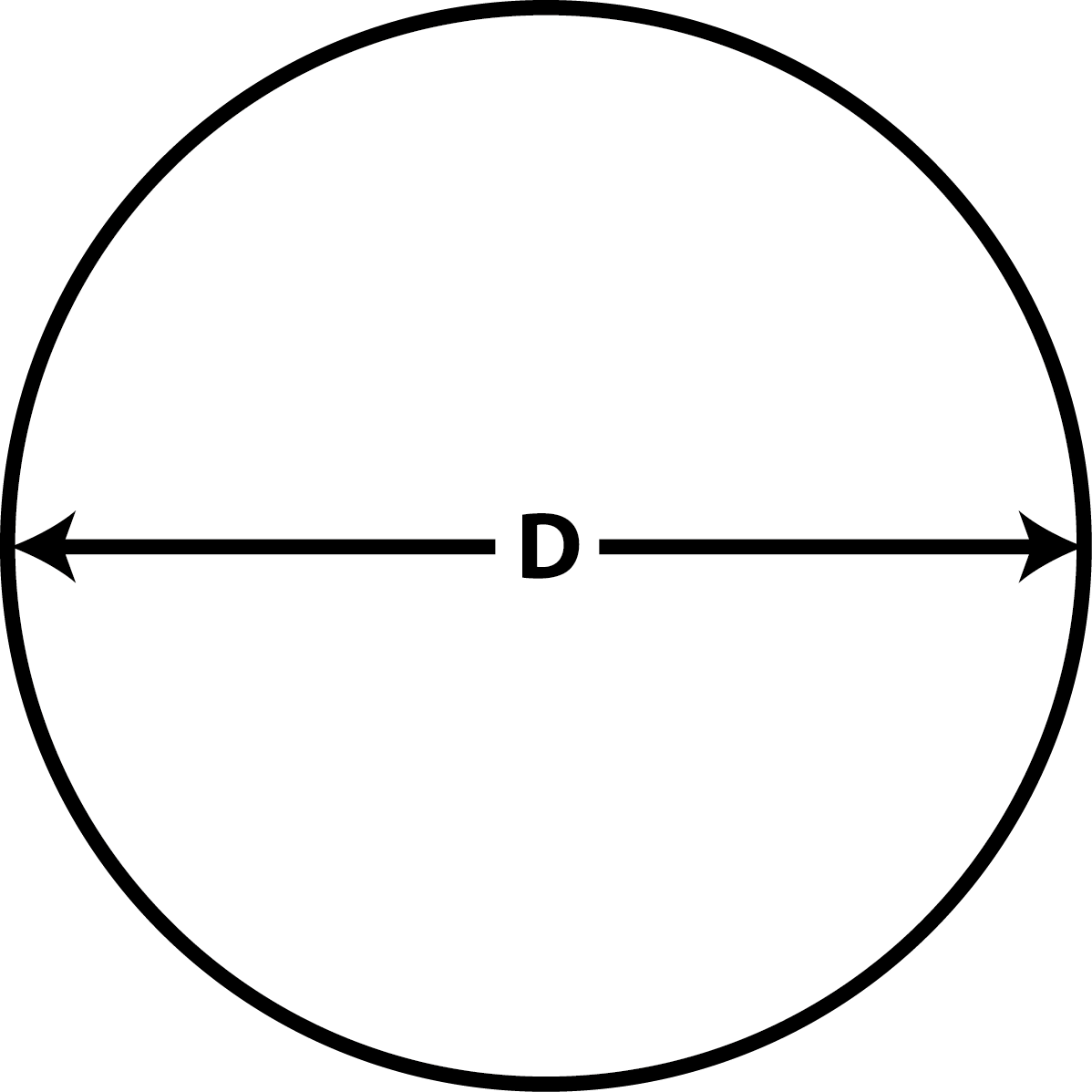
Die Objektivöffnung (Symbol: D) wird hä kurz als „Öffnung“ bezeichnet. Die Objektivöffnung ist der Durchmesser der Objektivlinse bzw. des Hauptspiegels. Sie wird häufig in Zoll angegeben.
Für die Umrechnung der Einheiten gilt: 1' (1 Zoll) = 2,54 cm.
Je größer die Objektivöffnung ist, desto mehr Licht kann eingefangen werden. Für die visuelle Beobachtung bedeutet dies, dass schwächere Objekte wahrgenommen werden können. Bei der Astrofotografie wird bei einer großen Objektivöffnung eine kürzere Belichtungszeit benötigt, um das gleiche Ergebnis zu erzielen wie mit einer kleineren Objektivöffnung.
|
|
|
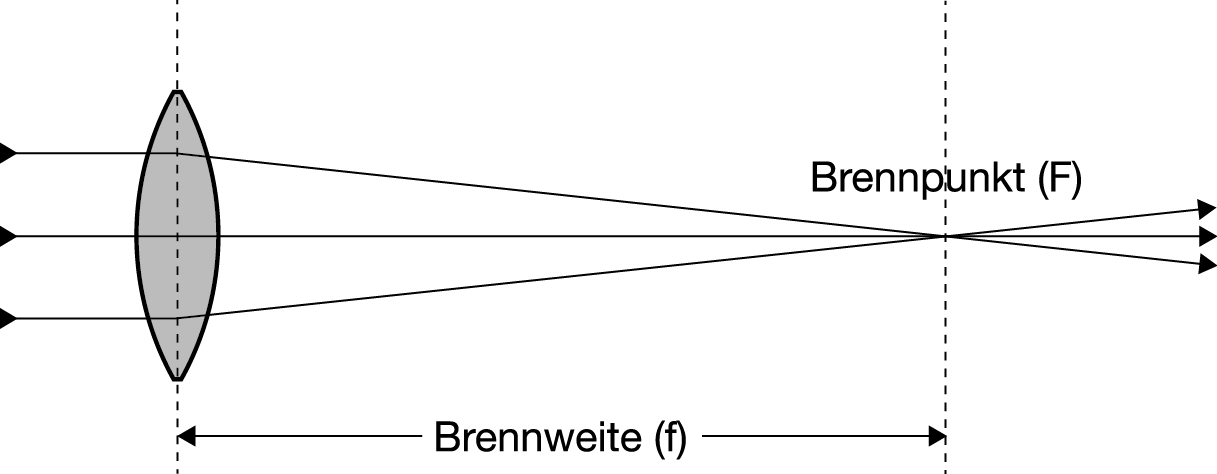
Brennweite einer beidseitig nach außen gewölbten (bikonvexen) Linse
|
|
|
|
|
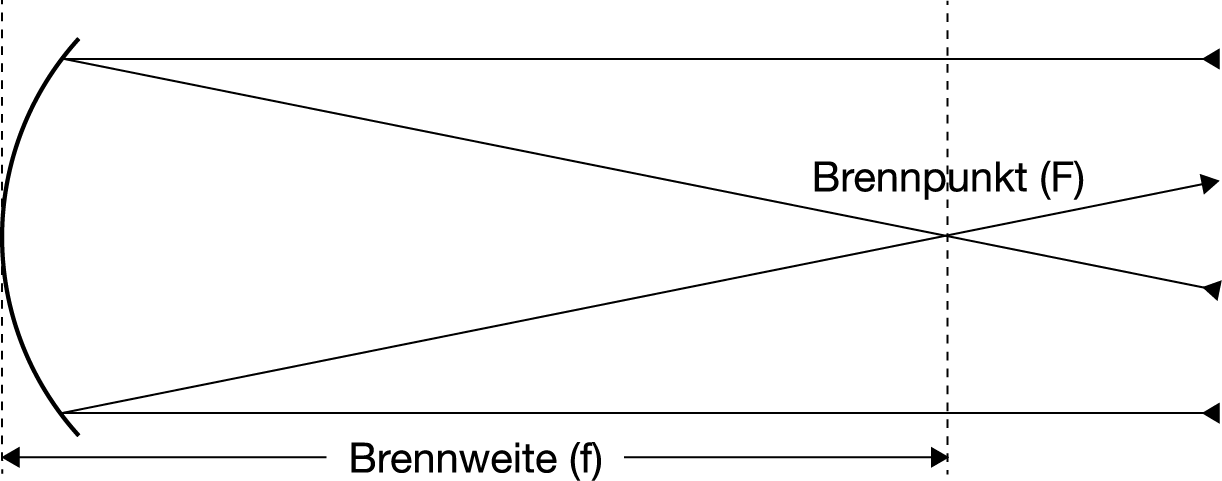
Brennweite eines nach innen gewölbten (konkaven) Spiegels
|
Die Brennweite (Symbol: f) eines Teleskops oder Okulars gibt an in welcher Entfernung von der ersten Objektivlinse bzw. vom Hauptspiegel parallel eintreffende Lichtstrahlen in einem Punkt vereinigt werden. Dieser Punkt wird Brennpunkt (lat.: focus) genannt (Symbol: F).
Die Brennweite bestimmt die Vergrößerung, die bei visueller Beobachtung mit einem bestimmten Okular erzielt werden kann. Hierbei gilt: Je größer die Objektivbrennweite, desto größer ist die Vergrößerung bei gleicher Okularbrennweite
Auf der rechten Seite befinden sich schematische Darstellungen der Brennweite für eine beidseitig nach außen gewölbte (bikonvexe) Linse und einen nach innen gewölbten (konkaven). Bei diesen Optiken handelt es sich um die in modernen Teleskopen am häufigsten verwendeten.
Das Öffnungsverhältnis (Symbol: o) ist das Verhältnis von Objektivöffnung (D) und Brennweite (f). Wie bei Kameraobjektiven wird es in der Regel mit 1 : x angegeben. Das Öffnungsverhältnis wird nach folgender Formel berechnet:
In der Regel wird Öffnungsverhältnis in der Bruchdarstellung und nicht als Dezimalzahl angegeben. Hierbei wird der Bruch so gekürzt, dass im Zähler eine Eins steht, was durchaus zur Folge haben kann, dass im Nenner eine Dezimalzahl steht.
Rechenbeispiele:
Für ein Teleskop mit 100 mm Objektivöffnung und 1000 mm Brennweite:
Für ein Teleskop mit 100 mm Objektivöffnung und 850 mm Brennweite:
|
|
|
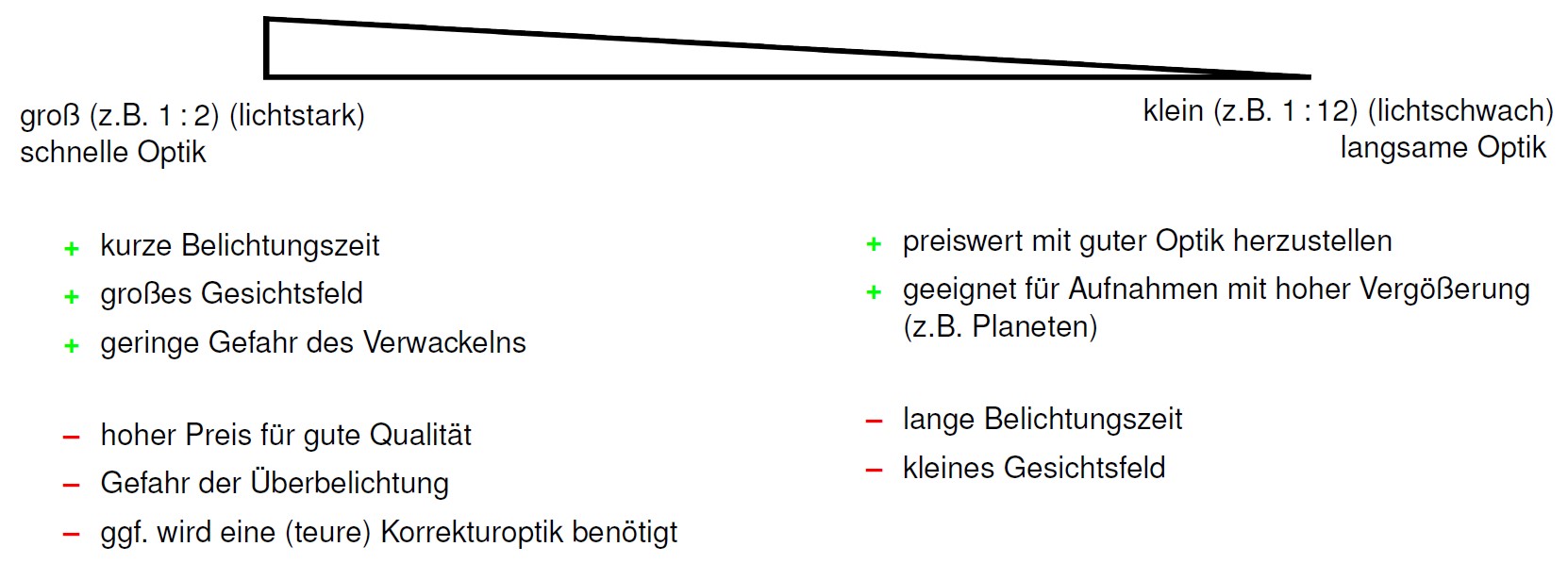
Vor- und Nachteile kleiner bzw. großer öffnungsverhältnisse
|
In der Umgangssprache wird häufig von einem großen bzw. einem kleinen Öffnungsverhältnis gesprochen.
Hier ist es wiederum hilfreich, wenn man den Bruch 1 : x in eine Dezimalzahl umwandelt. Das Ergebnis wird immer kleiner als eins sein, die Begriffe „groß“ und „klein“ sind hier also relativ. Ein Öffnungsverhältnis von 1 : 4 (=0,25) ist also groß und ein Öffnungsverhältnis von 1 : 20 (=0,05) ist klein.
Teleskope mit großem Öffnungsverhältnis werden auch als schnelle Teleskope bezeichnet, weil man in der Astrofotografie eine kürzere Belichtungszeit braucht, um das gleiche Ergebnis zu erhalten als mit Teleskopen mit kleinem Öffnungsverhältnis, die auch als langsame Teleskope bezeichnet werden. Wenn ein Teleskop für fotografische Himmelaufnahmen genutzt werden soll, dann sollte die Wahl auf ein schnelles Teleskop mit großem Öffnungsverhältnis fallen. In der Astrofotografie gilt ein Öffnungsverhältnis von 1 : 5 als guter Kompromiss. Die folgende Grafik gibt einen kurzen Überblick über die Vor- und Nachteile großer und kleiner Öffnungsverhältisse
Für die visuelle Beobachtung spielt die Wahl des Öffnungsverhältnisses eine weniger große Rolle, da die Helligkeit des wahrgenommen Bildes durch die Wahl des Okulars, also durch die Vergrößerung (siehe unten) beeinflusst wird. Entscheidend sind hier das Gesichtsfeld und die Austrittspupille (siehe unten).
Die Austrittspupille ist beim astronomischen Fernrohr der Durchmesser des Strahlenbündels, das das Okular verlässt. Je größer die gewählte Vergrößerung, desto kleiner ist die Austrittspupille.
Eine identische Austrittspupille ist der Grund, warum bei der visuellen Beobachtung durch die Wahl eines geeigneten Okulars mit unterschiedlichen Teleskopen (Bauweise, Objektivöffnung und Brennweite) ein Bild gleicher Helligkeit auf der Netzhaut erzeugt werden kann. Es wird hier aber keine Aussage über die Größe des Bildes getroffen, da diese von der Vergrößerung abhängig ist.
Die Austrittspupille des Okulars sollte nicht größer sein als der Durchmesser der Pupille der Augen des Beobachters (ca. 6 - 8 mm), weil dann nicht mehr das gesamte Strahlenbündel auf die Netzhaut trifft und Licht verlorengeht.
Die Austrittspupille (Symbol: AP) ist der Quotient aus Objektivöffnung (D) und Vergrößerung (V) oder als Formel ausgedrückt:
Rechenbeispiel:
Für ein Teleskop mit 100 mm Objektivöffnung und 1200 mm Brennweite und ein Okular mit 60° tatsächlichem Gesichtsfeld und 20 mm Brennweite.
Die Vergrößerung (Symbol: V), die man mit einer bestimmten Kombination von Objektiv und Okular erreicht, ist der Quotient aus Brennweite des Objektives und Brennweite des Okulars oder als Formel ausgedrückt:
Theoretisch kann man, bezogen auf ein Objektiv mit einer bestimmten Brennweite, durch die Wahl eines entsprechenden Okulars, eine Vielzahl von Vergrößerungen erreichen. Aber nicht jede Vergrößerung ist wirklich sinnvoll, denn durch die Physik und die Eigenschaften des menschlichen Auges sind hier Grenzen gesetzt. Es gibt also, bezogen auf die Brennweite des Objektivs, ein eine maximal sinnvolle Vergrößerung und eine minimal sinnvolle Vergrößerung.
Die maximal sinnvolle Vergrößerung wird durch unser Auge bestimmt. Wenn die Austritspupille, also das Strahlenbündel, das das Okular verlässt, weniger als 0,5 mm Durchmesser hat, dann wird das Bild, das man sieht zwar größer, aber auch unschärfer. Der Beobachter sieht also nicht mehr Details als mit einer etwas geringeren Vergrößerung. Der Grund hierfür ist die Verteilung der Sehzellen auf der Netzhaut.
Die maximal sinnvolle Vergrößerung entspricht der doppelten Objektivöffnung in Millimetern. Als Formel ausgedrückt also:
Rechenbeispiel:
Für ein Teleskop mit 100 m Objektivöffnung und 1200 mm Brennweite.
Wenn man das Ergebnis dieser Berechnung nun in die oben genannte Formel für die Vergrößerung einsetzt, dann kann man ausrechnen, welche minimale Brennweite für ein Okular, das man sich kaufen möchte, sinnvoll ist.
Es ist also nicht sinnvoll für ein Teleskop mit 100 m Objektivöffnung und 1200 mm Brennweite ein Okular mit einer Brennweite von weniger als 6 mm anzuschaffen.
Die minimal sinnvolle Vergrößerung wird durch das Auge des Beobachters bestimmt. Wenn das Auge voll an die Dunkelheit angepasst ist und die Pupillen bis zu ihrem maximalen Durchmesser geöffnet sind, dann beträgt der Durchmesser der Pupille 6-8 mm. Der tatsächliche Durchmesser der Pupille hängt von der individuellen Veranlagung und vom Lebensalter ab. Je älter ein Mensch wird, desto weniger können sich die Pupillen öffnen.
Wenn die Austritspupille, also der Durchmesser des Strahlenbündels, das das Okular verlässt, größer als die Öffnung der Pupille (6-8 mm) ist, dann kann nicht mehr das gesamte Gesichtsfeld überblickt werden. Die minimal sinnvolle Vergrößerung berechnet sich, wenn man von einem Mittelwert von 7 mm für die Öffnung der Pupille ausgeht, wie folgt:
Rechenbeispiel:
Für ein Teleskop mit 100 m Objektivöffnung und 1200 mm Brennweite.
Wenn man das Ergebnis dieser Berechnung nun in die oben genannte Formel für die Vergrößerung einsetzt, dann kann man ausrechnen, welche maximale Brennweite für ein Okular, das man sich kaufen möchte, sinnvoll ist.
Es ist also nicht sinnvoll für ein Teleskop mit 100 m Objektivöffnung und 1200 mm Brennweite ein Okular mit einer Brennweite von mehr als 86 mm anzuschaffen.
Das tatsächliche Gesichtsfeld beschreibt den Himmelsausschnitt, den man mit einer bestimmten Kombination von Teleskop und Okular sehen kann. Das tatsächliche Gesichtsfeld wird in Grad angegeben.
Bei der Beobachtung von Objekten mit großer Flächenausdehnung kann hilfreich das tatsächliche Gesichtsfeld im Vorfeld zu berechnen, denn je größer die gewählte Vergrößerung ist, desto kleiner wird das tatsächliche Gesichtsfeld. Hierbei erspart man sich umständliches Herumprobieren und unter Umständen ein mehrmaliges Wechseln des Okulars. Zwei Beispiele für Objekte mit großer Flächenausdehnung sind: Der Vollmond scheinbaren Durchmesser von einem halben Grad und der berühmte Orionnebel mit einem schienbaren Durchmesser von etwas mehr als einem Grad.
Das tatsächliche Gesichtsfeld ist der Quotient aus scheinbarem Gesichtsfeld des Okulars und der Vergrößerung oder als Formel ausgedrückt:
Rechenbeispiel:
Für ein Teleskop mit 100 mm Objektivöffnung und 1200 mm Brennweite und ein Okular mit 60° tatsächlichem Gesichtsfeld und 20 mm Brennweite.
Das scheinbare Gesichtsfeld ist eine konstruktive Eigenschaft des Okulars. Sie gibt den Öffnungswinkel an, den man sieht, wenn man nur durch das Okular (ohne Fernrohr) schaut. Der Öffnungswinkel variiert je nach Okulartyp. Bei höherwertigen Okularen ist der Öffnungswinkel in der Produktbeschreibung angegeben und häufig auch auf das Okular selber aufgedruckt. Das scheinbare Gesichtsfeld wird, wie das tatsächliche Gesichtsfeld auch, in Grad angegeben.
Hierbei gilt: Je größer das scheinbare Gesichtsfeld des Okulars ist, desto größer ist auch das tatsächliche Gesichtsfeld.
Das Auflösungsvermögen wird auch als Trennschärfe bezeichnet. Das Auflösungsvermögen gibt an wie groß der Winkelabstand zwischen zwei Objekten oder zwei Details (z.B. auf einer Planetenberläche) sein darf um diese als zwei Einzelheiten wahrnehmen zu können. Der Winkelabstand wird in Bogensekunden (Symbol: ’’) angegeben.
Das Auflösungsvermögen eines Teleskops ist von der Objektivöffnung abhängig. Theoretisch kann also mit einer großen Objektivöffnung ein sehr hohes Auflösungsvermögen erreicht werden. Durch die Luftunruhe ist das Auflösungsvermögen meistens jedoch auf etwa 1’’ begrenzt. In der Praxis bedeutet das, dass Teleskope mit einer Öffnung von mehr als 120 mm keinen Gewinn beim Auflösungsvermögen bringen. Die großen Profiteleskope verfügen über eine sogenannte adaptive Optik mit deren Hilfe die Luftunruhe kompenisert werden kann und das Auflösungsvermögen an den theoretischen Wert heran gebrach werden kann.
Die Lichbeugung ist abängig von der Wellenlänge. Um eine einfach handhabbare Faustformel für die Berechnung des Auflösungsvermögens zu erhalten wird mit einer Wellenlänge von 550 nm gerechnet, bei der auch die höchste Empfindlichkeit des menschlichen Auges liegt. Diese Faustformel lautet:
Rechenbeispiel:
Für ein Teleskop mit 100 mm Objektivöffnung.
Die folgende Tabelle zeigt das theoretische Auflösungsvermögen für einige im Amateurbereich häufig verwendete Teleskopöffnungen
| Objektivöffnung | theoretisches Auflösungsvermögen |
Auflösungsvermögen in der Praxis |
|
|---|---|---|---|
| mm | Zoll | ||
| 60 | 2,4 | 2,3’’ | 2,3’’ |
| 70 | 2,8 | 1,97’’ | 1,97’’ |
| 80 | 3,1 | 1,73’’ | 1,73’’ |
| 100 | 4 | 1,38’’ | 1,38’’ |
| 120 | 4,7 | 1,15’’ | 1,15’’ |
| 130 | 5,1 | 1,06’’ | 1,06’’ |
| 150 | 6 | 0,92’’ | 1’’ |
| 200 | 8 | 0,69’’ | 1’’ |
| 250 | 10 | 0,55’’ | 1’’ |
Die Informationen auf dieser Seite sind auch als zweiteiliges Video auf YouTube verfügbar. Achtung: Beim Start der Videos werden automatisch die Gesch&aouml;ftsbedingungen von YouTube akzeptiert.
Teil 1
Teil 2
Aktualisiert am 2. Januar 2025 von Martina Haupt