 Zum Seitenanfang
Zum Seitenanfang
Das das Thema „Winkelmaß und Bogenmaß“ ist wegen der Übersichtlichkeit in mehrere Abschnitte unterteilt. Hier eine kurze Übersicht, die das Auffinden einzelner Informationen erleichtern soll.
> Gradmaß
• Bogenmaß
Das Winkelmaß wird zur Angabe der Winkelweite eines ebenen Winkels benutzt, und kommt sowohl als physikalische Größe als auch in der Mathematik zur Anwendung. Je nach Anwendung werden verschiedene Maße und Einheiten benutzt.
Der Vollwinkel ist in Deutschland und in der Schweiz eine gesetzliche Einheit, und findet im Messwesen für die physikalische Größe Winkelweite Anwendung. Der Vollwinkel ist derjenige Winkel, um den ein Strahl um seinen Anfangspunkt gedreht muss, damit er zum ersten Mal wieder seine ursprüngliche Lage erreicht. Die Einheit Vollwinkel besitzt kein Einheitszeichen, und dezimale Vielfache dürfen nicht mit SI-Vorsätzen gebildet werden.
Der Grad ist eine Hilfsmaßeinheit für den Größenwert eines ebenen Winkels, die es erlaubt nicht ganzzahlige Vielfache des Vollwinkels darzustellen. 1 Grad ist definiert als der 360. Teil des Vollwinkels, d.h. 1 Vollwinkel = 360°. Untereinheiten des Grads sind die Bogenminute und die Bogensekunde, die sich nicht, wie der Name vermuten lässt auf das Bogenmaß beziehen. Das Einheitszeichen für den Grad ist °, das ist ein kleiner, hochgestellter Kreis, der ohne Zwischenraum an die letzte Ziffer angehängt wird. SI-Vorsätze wie z.B. Milli- oder Kilo- sind auf den Grad nicht anwendbar.
Es gibt mehrere Möglichkeiten Bruchteile von Graden darzustellen. Die Angabe von Bruchteilen von Graden kann einerseits im Dezimalsystem, also im Zehnersystem, das auf der Basiszahl 10 beruht, erfolgen. Andererseits kann die Angabe von Graden auch im Sexagesimalsystem erfolgen, das die Zahl 60 als Basiszahl hat. Es ist aber auch möglich eine Kombination aus dezimaler und sexagesimaler Darstellung für die Darstellung von Bruchteilen von Graden zu verwenden.
Darstellung im Dezimalsystem
Bei der Darstellung im Dezimalsystem wird die Maßzahl als Dezimalzeichen mit dem Einheitszeichen ° angegeben.
Beispiel: 35,24°
Darstellung im Sexagesimalsystem*
Im Sexagesimalen System,das, wie bereits erwähnt, die Zahl 60 als Basiszahl hat, gilt:
1° = 60' = 3600''
1' = 60''
daraus ergeben sich folgende Darstellungen für die Darstellung von Bruchteilen von Graden:
Grad und Bogenminuten: ggg° mm'' − Beispiel: 185° 18'
Grad, Bogenminuten und Bogensekunden: ggg° mm'' ss'' − Beispiel: 164° 49' 17''
Darstellung in der Kombination von Sexagesimalsystem und Dezimalsystem*
Grad und Bogenminuten: ggg° mm,m'' − Beispiel: 185° 18,5'
Grad, Bogenminuten und Bogensekunden: ggg° mm'' ss,s'' − Beispiel: 164° 49' 17,4''
* Für die oben stehenden Beispiele wurden folgende Symbole und Einheitszeichen benutzt:
|
In der Astronomie ist das Zeitmaß, das oft auch als Stundenmaß bezeichnet wird, die Angabe eines Winkels in Einheiten der Zeit, d.h. in Stunden, Minuten und Sekunden. Ein Vollwinkel von 360° entspricht im Zeitmaß 24 Stunden.
Um zu vermeiden, dass es zu einer Verwechslung von Angaben im Zeitmaß und Angaben im Gradmaß kommt werden bei Angaben im Zeitmaß häufig die hochgestellten Zeiteinheitszeichen verwendet. Eine Angabe im Stundenmaß wird also Beispielsweise als 3h 25m 13s notiert. Im Gradmaß würde man den gleichen Winkel als 51° 18' 15'' darstellen.
In der Astronomie wird das Zeitmaß für die Angabe der Sternzeit, der Rektaszension und des Stundenwinkels angewandt.
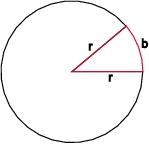
Das Bogenmaß ist bei vielen Berechnungen in der Mathematik und in der Physik sehr zweckmäßig. Da die Werte jedoch sehr unanschaulich sind wird für den Alltagsgebrauch meist das Gradmaß verwendet. Trotzdem soll das Bogenmaß an dieser Stelle kurz erwähnt werden.
Das Bogenmaß ist eine dimensionslose Zahl. Um eine Unterscheidung vom Winkelmaß zu gewährleisten kann der Zusatz rad (für Radiant) an die Zahl angehangen werden. Das Bogenmaß ist definiert als das Verhältnis der Länge des Kreisbogens b zum Radius r. Wenn der Radius r des Kreises gleich 1 ist, dann ist die Länge des Kreisbogens gleich b. Für den Umfang eines Kreises gilt: U=2 π r. Daraus ergibt sich, dass das Verhältnis von Kreisumfang zum Kreisradius gleich 2π ist. Der Vollwinkel beträgt deshalb im Bogenmaß 2π.
Erstellt am 28. November 2009 von Martina Haupt