 Zum Seitenanfang
Zum Seitenanfang
Eine Längenmaßeinheit dient zur Angabe oder Messung einer Strecke bzw. eines Abstandes. Zusammen mit der Maßzahl muss immer eine Dimension angegeben werden, die das Einheitensystem widerspiegelt, auf das sich die Maßzahl bezieht. Hieraus lässt sich unschwer folgern, dass es verschieden Einheitensyseme für das Längenmaß gibt. Auf dieser Seite wird auf die Längenmaßeinheiten eingegangen, die in der Astronomie verbreitet sind.
Bei sehr kleinen oder sehr großen Maßzahlen wird die Darstellung der Zahl schnell unübersichtlich. Deshalb benutzt man in solchen Fällen Vorsilben, die für bestimmte Bruchteile oder Vielfache stehen, oder man schreibt die Maßzahl in der Zehnerpotenz-Schreibweise. Auf Beides wird am Ende der Seite eingegangen.
Das es, wie im vorherigen Absatz erwähnt, verschiedene Einheitensysteme für das Längenmaß gibt, hier eine kurze Übersicht, die das Auffinden eines bestimmten Einheitensystems erleichtern soll.
• Das Zoll
• Die Astronomische Einheit (AE)
> Darstellung als Zehnerpotenz
Der oder das Meter (laut Duden ist beides korrekt) ist die Basiseinheit für die Länge im internationalen Einheitensystem SI. Das Einheitssymbol für den Meter ist der Kleinbuchstabe m, der Dimensionsname ist Länge und das Dimensionsymbol ist L.
Der Meter wurde Ende des 18. Jahrhunderts auf einen Beschluss der französischen Nationalversammlung eingeführt und wurde definiert als der zehn-millionste Teil der Entfernung vom Nordpol über Paris zum Äquator. Damit wurde eine Längeneinheit geschaffen, die nicht mehr von Maßen des menschlichen Körpers abhing wie z.B. Daumenbreit, Handbreit, Elle oder Fuß.
Da die Erde aber keine ideale Kugel ist, sondern eine unregelmäßige Form hat, erwies sich diese Definition als ungeeignet. Außerdem wurden bei späteren Messungen immer wieder leicht abweichende Werte ermittelt. Um eine feste Bezugsgröße zu haben wurde, basierend der Vermessung des Meridianbogens, das Urmeter definiert und auf Grundlage dieses Wertes wurde im Jahr 1795 ein erster Prototyp des Urmeters aus Messing hergestellt.
Basierend auf einer neuen Vermessung wurde 1799 dann ein zweiter Urmeter eingeführt, der auch als definitiver Urmeter bezeichnet wird.
Der dritte, internationale Prototyp des Urmeters wurde am 26. September 1889 von der Generalkonferenz für Maß und Gewicht (CGPM) eingeführt und bestand aus einer Platin-Iridium-Legierung. 30 Kopien dieses Urmeters wurden an Eichinstitute vergeben. Das Urmeter war bis 1960 gültig.
Beim Kopieren des Urmeters kam es zwangsläufig zu minimalen Abweichungen und bei den regelmäßigen Vergleichen der Kopien untereinander und mit dem Original bestand das Risiko von Beschädigungen. Der Meterprototyp aus der Platin-Iridium-Legierung ist also grundsätzlich nicht unvergänglich
Deshalb wurde der Meter im Jahr 1960 neu definiert: Ein Meter war nun das 1 650 763,73-fache der Wellenlänge der von Atomen des Nuklids 86Kr beim Übergang vom Zustand 5d5 zum Zustand 2p10 ausgesandten, sich im Vakuum ausbreitenden Strahlung. Damit war der Meter die erste Basiseinheit, die auf einer Naturkonstanten beruhte. Mit der notwendigen Laborausstattung konnte die Länge des Meters nun an jedem Ort reproduziert werden.
Am 20. Oktober 1983 beschloss die 17. Generalkonferenz für Maß und Gewicht (CGPM) nicht mehr die Lichtgeschwindigkeit zu messen und zu präzisieren, sondern statt dessen die Längeneinheit Meter über den 1975 festgelegten Standardwert für die Lichtgeschwindigkeit zu definieren. Damit wurde ein Meter definiert als die Strecke, die das Licht im Vakuum innerhalb des Zeitintervalls von 1/299 792 458 Sekunden durchläuft.
Die Längenmaßeinheit Meter ist auch in der Astronomie gebräuchlich. Bei sehr großen Längen und Strecken werden häufig auch andere Längenmaßeinheiten, wir das Lichtjahr oder die Parsec, benutzt, die es erlauben mit sehr viel kleineren Maßzahlen zu arbeiten. Bei „kleineren“ Teleskopen, die unter anderem im Amateurbereich genutzt werden, wird der Durchmesser der Objektivlinse oder der Durchmesser des Fangspiegels häufig in Zoll angegeben.
Das Zoll bezeichnet eine Vielzahl von alten Maßeinheiten im Bereich von zwei bis vier Zentimetern. Zum Beispiel wurde das englische Zoll im Jahre 1234 von Eduard II. von England als die Länge dreier hintereinander liegender Gerstenkörner festgelegt. Vielfach war das Zoll aber auch als „Daumenbreit“ definiert und war meist der 12. Teil eines Fußes.
Bis Mitte des 20. Jahrhunderts wichen das englische und das amerikanische Zoll leicht voneinander ab. Es wurde jedoch ein Kompromiss gefunden und 1959 wurde das Zoll auf genau 25,4 mm festgelegt. Das internationale Zoll wird heute hauptsächlich in den USA als übliches Längenmaß verwendet.
Das internationale Zoll, das im Englischen als Inch bezeichnet wird, entspricht einer Länge von 25,4 mm. Gemäß ISO 31-1 Annex A ist das Einheitszeichen für das englische Zoll in. Gebräuchlicher ist aber das Zollzeichen: ″.
Für festgelegte Größenangaben wird das Zoll auch heute noch in der Technik verwendet. Für Teilangaben werden in der Regel Brüche verwendet wie z.B. 1/2, 1/4, 1/8 oder 1/16; aber auch Angaben wie 3/8 oder 5/16 sind geläufig.
In der Astronomie ist in einigen Bereichen, beispielsweise für die Angabe für Öffnungen von Teleskopen, das internationale Zoll gebräuchlich.
So wird ein Teleskop mit 10 cm Öffnung häufig auch als 4-Zöller bezeichnet oder ein Teleskop mit 15 cm Öffnung als 6-Zöller.
Auch das Steckmaß für Okulare und der Durchmesser von Filtern, die Okularseitig angebracht werden, wird in Zoll angegeben.
Gebräuchlich sind hier 1 1/4 Zoll (31,8 mm) und 2 Zoll (50,8 mm).
1 in = 1″ = 25,4 mm = 2,54 cm
Die Astronomische Einheit ist eine in der Astronomie häufig benutzte Einheit. Sie wird zum Beispiel gerne für Entfernungsangaben innerhalb unseres Sonnensystems benutzt, da sich so „handliche“, also gut lesbare, Zahlenwerte ergeben.
Das Internationale Büro für Maß und Gewicht (IBMG) und die Internationale Astronomische Union (IAU) empfehlen für die Astronomische Einheit das Einheitszeichen au; abgeleitet von der englischen Bezeichnung Astronomical Unit. In der deutschsprachigen Literatur hat sich allerdings die Verwendung von AE, oder AU als Einheitszeichen durchgesetzt.
Seit 2012 ist die Astronomische Einheit definert als:
1 AE/AU = 149 597 870 700 m ≈ 149,6 Millionen Kilometer
Historisch wurde die Astronomische Einheit als die Länge der großen Halbachse der Umlaufbahn der Erde um die Sonne definiert, das ist der Abstand vom Erdmittelpunkt zum Mittelpunkt der Sonne. Dieser Wert wurde hauptsächlich aus Parallaxenmessungen mit dem Erdbahnradius als Basislinie abgeleitet. Diese Messungen, die als Ergebnis die Entfernung eines Objekt relativ zum Erdbahnradius lieferten, waren auf Grund der verwendeten Messmethoden genauer als die absoluten Werte.
1967 wurde die Astronomische Einheit von der Internationalen Astronomischen Union (IAU) neu definiert. Nach dieser Neudefinition ist eine Astronomische Einheit der Radius einer kreisförmigen Umlaufbahn, auf der ein hypotetisches Objekt mit vernachlässigbarer Masse und frei von Störungen die Sonne in 2 π / k Tagen umläuft. Dabei ist k die Gaußsche Gravitationskonstante (k=0,01720209895). Dieser Wert der Astronomischen Einheit wurde mit Hilfe von Radar- und anderen Distanzmessungen von der Erde zu den Nachbarplaneten und zu Raumsonden bestimmt. Demnach entsprach eine Astronomische Einheit 149 597 870 691 m.
Durch die Anwendung moderner Messmethoden ist die Astronomische Einheit so genau bekannt, dass die Verwendung der Astronomische Einheit keine höhere Genauigkeit bietet als die Angabe im metrischen System. Deshalb wurde die Definition der Astronomischen Einheit aus dem Jahre 1967 aufgegeben und die Astronomische Einheit wurde, wie bereits oben erwähnt, im Jahr 2012 definiert als: 1 AE/AU = 149 597 870 700 m ≈ 149,6 Millionen Kilometer.
Die Astronomische Einheit ist keine gesetzliche Maßeinheit.
Sie gehört auch nicht zum internationalen Einheitssystem (SI), ist aber zum Gebrauch mit dem SI zugelassen.
1 AE/AU = 149 597 870 700 m ≈ 149,6 Millionen Kilometer
1 AE/AU = 0,0000158 LJ (Lichtjahre)
1 AE/AU = 0,000004848 pc = 4,848×10-6 pc (Parsec)
Ein Lichtjahr ist als die Strecke definiert, die eine elektromagnetische Welle in einem julianischen Jahr im Vakuum zurücklegt. Das Lichtjahr ist keine SI-Einheit, wird aber in der Astronomie häufig benutzt um Entfernungen anzugeben. Das Einheitszeichen für das Lichtjahr ist LJ.
Physikalisch betrachtet ist das Licht nichts Anderes als eine elektromagnetische Welle,
die sich mit endlicher Geschwindigkeit ausbreitet.
Im Falle des Lichtes wird die Ausbreitungsgeschwindigkeit im Vakuum als Lichtgeschwindigkeit
bezeichnet. Die Lichtgeschwindigkeit im Vakuum ist eine Naturkonstante und beträgt 299 792 458 m/s,
das sind 299 792,458 km/s.
Ein julianisches Jahr ist genau 365,25 Tage (=3 155 760 s) lang.
Daraus ergibt sich, dass das Licht im Vakuum in einem Jahr eine Strecke von 9 460 730 472 580,8 km zurücklegt.
1 LJ = 9 460 730 472 580,8 km
1 LJ = 63 241,077088071 AE/AU (Astronomische Einheiten)
1 LJ = 0,3066011058 pc (Parsec)
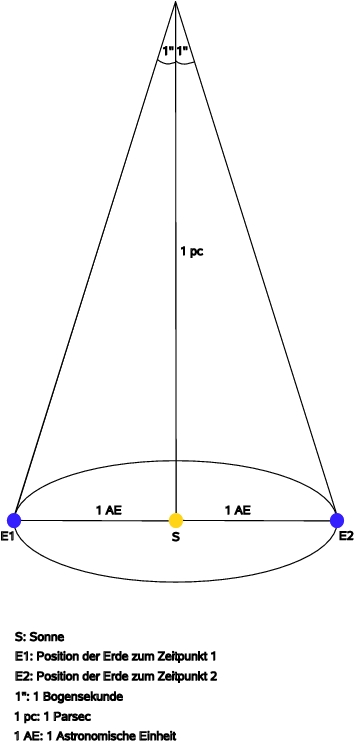
Die Parsec ist eine Längenmaßeinheit, die in der Astronomie für Entfernungsangaben benutzt wird. Das Einheitszeichen für die Parsec ist pc. Die Abkürzung „Parsec“ steht für Parallaxensekunde. Die Parsec ist, genau wie die astronomische Einheit und das Lichtjahr, keine SI-Einheit. Die Parsec wird in der Astronomie häufig benutzt um Entfernungen anzugeben, denn die Parallaxenmessung ist eine der grundlegenden Methoden zur Messung astronomischer Entfernungen.
Die Parsec ist definiert als die Entfernung eines Sterns, der eine jährliche Parallaxe von genau einer Bogensekunde aufweist. Anders herum ausgedrückt erscheint die Länge der großen Halbachse der Erde aus einer Entfernung von einer Parsec unter einem Winkel von einer Bogensekunde. In der Skizze links ist dies stark überzeichnet dargestellt.
Das Wort Parallaxe hat Seinen Ursprung im Griechischen und bedeutet soviel wie Abweichung. Die Parallaxe ist definiert als der Winkel zwischen zwei Geraden, die von verschiedenen Standorten auf ein Objekt gerichtet sind. Sie bezeichnet die scheinbare Änderung der Position eines Objekts, wenn der Beobachter seinen Standort ändert. Ein sehr anschauliches Beispiel ist der „Daumensprung“. Der Abstand der beiden verschiedenen Standorte wird durch den Augenabstand des Beobachters symbolisiert. Wenn man den nach oben gestreckten Daumen einer Hand wechselweise mit dem rechten und dem linken Auge betrachtet (das andere Auge wird geschlossen) scheint er vor dem Hintergrund hin und her zu springen. Dieser Sprung ist umso größer je geringer der Abstand des Daumens zum Gesicht ist
Übertragen auf astronomische Maßstäbe ist der Augenabstand eines Menschen viel zu gering um eine
Sternparallaxe messen. Deshalb wird die Länge der großen Halbachse der Erdbahn zugrunde gelegt.
Unter der Annahme, dass die Eigenbewegung des beobachteten Sterns innerhalb eines halben Jahres vernachlässigbar
klein ist, wird die Position eines Stern im Halbjahresabstand, also nach einem halben Erdumlauf um die Sonne,
zweimal vermessen. Die gemessene Parallaxe wird dann auf eine
Basislinienlänge von einer Astronomischen Einheit (1 AE) normalisiert. Wenn die auf diese Weise gemessene
Parallaxe genau eine Bogensekunde beträgt, dann ist der Stern genau eine Parsec von der Erde entfernt.
1 pc = 30 856 776 000 000 000 m = 3,0856776×1016 m
1 pc = 206 264 ,806 AE (Astronomische Einheiten)
1 pc = 3,26 LJ (Lichtjahre)
Sehr große bzw. sehr kleine Zahlen werden auf Grund der vielen Stellen, die benötigt werden um sie darzustellen, sehr schnell unübersichtlich. Die Zahlen lassen sich dann nur noch sehr schwer mit einem Blick erfassen und der Lesefluss, z.B. in einem Fachartikel wird gestört. Um diesem Problem aus dem Weg zu gehen kann man entweder Vorsilben benutzen, die der Maßeinheit vorangestellt werden, oder man kann die Zahl in der Zehnerpotenz-Schreibweise darstellen.
Die Vorsilben, die benutzt werden können um Vielfache oder Bruchteile von Zahlen darzustellen werden auch mit dem Fremdwort Präfixe bezeichnet. Für die Verwendung im Internationalen Einheitssystem (SI-System) sind Dezimal-Präfixe definiert, die auf Zehnerpotenzen mit ganzzahligem Exponenten basieren. Für jedem Präfix gibt es ein international einheitliches Symbol, das dem Einheitszeichen vorangestellt wird. Die Bedeutung der Vorsilben und die entsprechende Darstellung als Zehnerpotenz kann der unten stehenden Übersichtstabelle entnommen werden.
Das Dezimalsystem, das wir in der Regel zum Darstellen von Zahlen und zum Rechnen benutzen wird auch als Zehnersystem bezeichnet. Der Begriff Dezimalsystem leitet sich von dem lateinischen Wort Dezimus ab, das soviel wie „der Zehnte“ bedeutet. Schon aus der Bezeichnung Dezimalsystem lässt sich unschwer erahnen, dass die Zahl 10 in diesem, ursprünglich aus Indien stammenden, System eine wichtige Rolle spielt.
Die Darstellung von Zahlen als Zehnerpotenzen ermöglicht es auch sehr große oder sehr kleine Zahlen in einer kompakten Schreibweise darzustellen. Bei der Darstellung einer Zahl in der Zehnerpotenz-Schreibweise wird zuerst ein Faktor angegeben, bei dem nur eine Stelle vor dem Komma steht. Die anderen Ziffern werden als Dezimalstellen hinter dem Komma angegeben. Hinter diesem Faktor steht dann eine Potenz mit der Basis (=Grundzahl) Zehn und einem ganzzahligen Exponenten (Hochzahl). Ein positiver Exponent gibt an, wie oft der Faktor mit 10 multipliziert werden muss um die dargestellte Zahl so zu erhalten, wie man sie als „normale“ Dezimalschreibweise ausschreiben würde. Umgekehrt gibt ein negativer Exponent an wie oft der Faktor durch 10 geteilt werden muss, um die dargestellte Zahl so zu erhalten, wie man sie als „normale“ Dezimalschreibweise ausschreiben würde. Zum Beispiel wird die Zahl 5000 wird in der Zehnerpotenzschreibweise als 5 × 103 dargestellt, und die Zahl 0,005 wird als 5 × 10-3 dargestellt. Das Multiplikationszeichen zwischen dem Faktor und der Potenz wird in naturwissenschaftlichen Veröffentlichungen oft weggelassen. Eine Überischt über die Zehnerpotenzen und die den Zehnerpotenzen entsprechenden Vorsilben kann der unten stehenden Übersichtstabelle entnommen werden.
|
Aktualisiert am 21. Juli 2025 von Martina Haupt